만약 힙이 어떻게 동작하는지 이해하고 싶다면만 바꿔보세요.

만약에 힙이 어떻게 동작하는지 정확히 알 필요가 없다면 기본적으로 제공되는 heapq를 사용하여 업무를 처리할 수 있습니다.

하지만 힙이 어떻게 내부적으로 동작하는지 이해하길 원한다면, 힙을 처음부터 코딩하여 배우는 것을 추천할 수도 있어요.

힙(Heap)이란?

힙에는 2 종류가 있어요 — 최소 힙과 최대 힙

최소 힙은 이진 트리입니다. 부모 노드가 항상 자식 노드보다 작거나 같은 경우.

최대 힙도 이진 트리입니다. 부모 노드가 항상 자식 노드보다 크거나 같은 경우.

시각화

아래 이미지는 현재 작성 중인 HTML 테이블입니다.

참고 - 왼쪽 자식 또는 오른쪽 자식 중 어느 쪽이 더 큰지는 중요하지 않습니다.

중요한 것은 부모가 다음과 같아야 합니다:

• 자식보다 작거나 같아야 함 (최소 힙)
• 자식보다 크거나 같아야 함 (최대 힙)

힙이란 무엇인가요?

그것은 우선 순위 큐입니다.

최소 힙에서 가장 작은 값이 항상 다음에 나옵니다.

최대 힙에서 가장 큰 값이 항상 다음에 나옵니다.

어떤 순서로 넣거나 빼도 상관 없어요.

리스트를 사용할 수 없는 이유는?

사용할 수는 있지만 시간적으로 효율적이지 않아요.

우선 순위 큐로서 리스트 사용하기:

• 새로운 요소 삽입 → O(1) 상수 시간
• 가장 높은 우선 순위 요소 제거 → O(n) 선형 시간

힙을 사용하면:

• 새로운 요소 삽입 → O(log n) 로그 시간
• 가장 높은 우선 순위 요소 제거 → O(log n) 시간

많은 요소가 있다면, 리스트 대신 힙을 사용하는 것이 더 시간효율적입니다.

또한 코딩 면접을 볼 때, 우선 순위 큐로서 목록을 사용하는 것보다 힙을 사용하는 것이 더 많은 점수를 획들할 수 있어요.

데모 시간

간단하게, 예시로서 최소 힙을 사용해봐요.

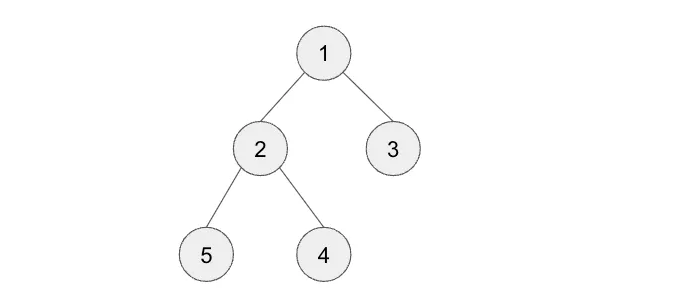
1) 이 민 힙에 6을 삽입하기

단계 1 — 새로운 노드 6을 다음 사용 가능한 공간에 삽입하기

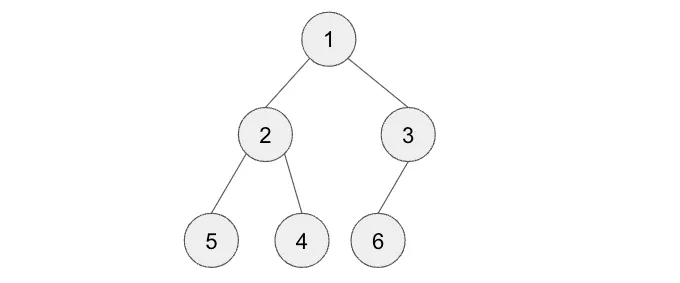
단계 2 — 부모보다 큰지 확인하기.

그리고 지금 힙은 괜찮기 때문에, 아무것도하지 않아도 됩니다.

2) 이 최소 힙에 0을 삽입

단계 1 - 새로운 노드 0을 다음 사용 가능한 공간에 삽입하기만 하면 됩니다.

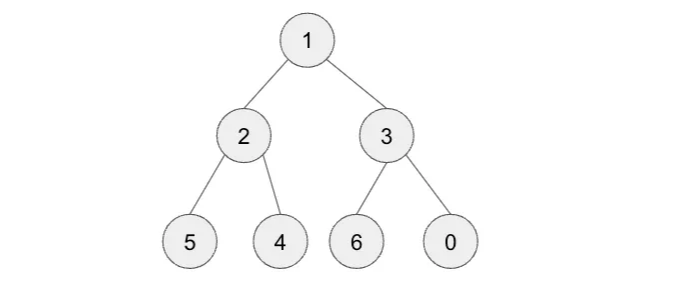
Step 2 - 부모보다 큰지 확인해 봅니다.

하지만 0은 아닙니다. 0은 부모인 3보다 작습니다. 이는 최소 힙의 규칙을 위배합니다 - 모든 부모는 자식들보다 작거나 같아야 합니다.

Step 3 - 0과 3을 교체합니다

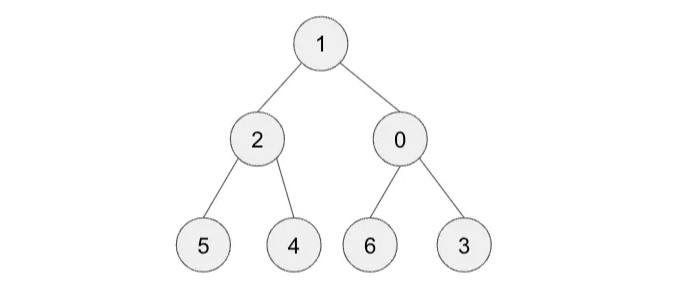
Step 4—단계 2와 3을 재귀적으로 반복합니다. 부모보다 0이 큰지 루트까지 도달한 것에 상관없이

이 경우, 추가로 한 번 더 전환해야 합니다

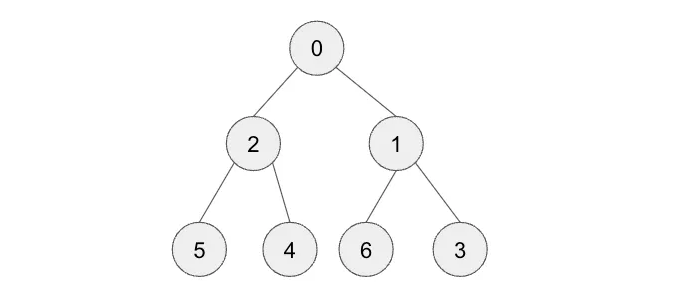
이 시점에서, 힙은 모든 부모 ≤ 자식을 만족시키기 때문에 더 이상 조치를 취하지 않습니다.

3) 가장 작은 원소를 제거하기 (또는 팝하기)

단계 1 — 우리는 먼저 루트 노드 0을 최신 노드 3과 교환합니다

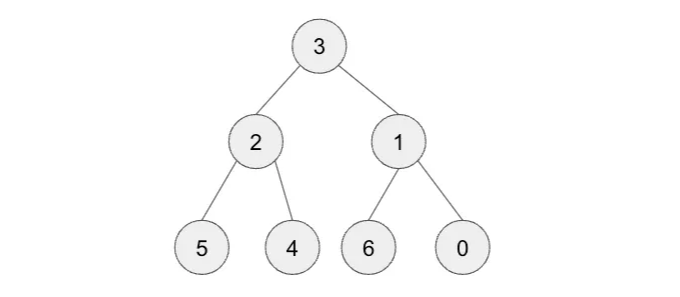
단계 2 — 노드 0을 제거합니다

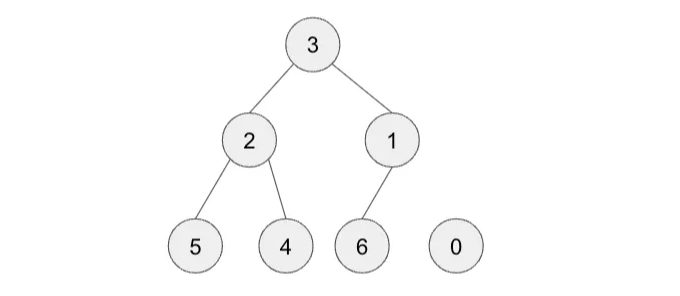
Now, 3 is the root, which isn’t correct. We need to fix our heap.

Step 3 — switch 3 with its smaller child until the min heap condition is fulfilled

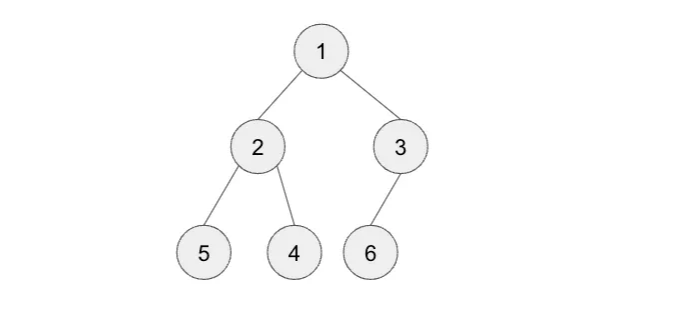
그리고 이 시점에 우리의 최소 힙은 다시 복구되었습니다.

코드 (최소 힙)

class Node:
    def __init__(self, val):
        """ l -> left
            r -> right
            p -> parent
        """
        self.val = val
        self.l = self.r = self.p = None

    def adopt(self, side: str, val: int):
        """ 자식 노드를 생성합니다.
            side: 'l' 또는 '  r'
            val: 자식 노드의 값
        """
        setattr(self, side, Node(val))
        getattr(self, side).p = self

    def push(self, val):
        """ 힙에 새로운 값을 추가합니다. """
        def repair(node):
            # 부모가 자식보다 작거나 같은 조건을 충족하는지 확인
            if node.p is None or node.val > node.p.val: return
            node.val, node.p.val = node.p.val, node.val
            repair(node.p)

        q = [self]
        while q:
            cur = q.pop(0)
            if cur.l is None: return cur.adopt('l', val), repair(cur.l)
            if cur.r is None: return cur.adopt('r', val), repair(cur.r)
            if cur.l: q.append(cur.l)
            if cur.r: q.append(cur.r)

    def pop(self):
        """ 힙에서 가장 작은 요소를 제거하고 반환합니다. """
        def get_leaf(node):
            # 가장 오른쪽에 있는 잎 노드를 가져옵니다 (왼쪽도 동작합니다)
            q = [node]
            while q:
                cur = q.pop(0)
                if (cur.l, cur.r) == (None, None): return cur 
                if cur.r: q.append(cur.r)
                if cur.l: q.append(cur.l)

        def repair(n):
            # 부모가 자식보다 작거나 같은 조건을 충족하는지 확인
            if (n.l and n.l.val < n.val) or (n.r and n.r.val < n.val):
                if n.r is None or n.l.val < n.r.val:
                    n.val, n.l.val = n.l.val, n.val
                    repair(n.l)
                elif n.l is None or n.r.val < n.l.val:
                    n.val, n.r.val = n.r.val, n.val
                    repair(n.r)
                
        leaf = get_leaf(self)
        leaf.val, self.val = self.val, leaf.val

        if leaf.p.l == leaf: leaf.p.l = None
        else: leaf.p.r = None

        repair(self)
        return leaf.val

결론 🎉

테이블 태그를 Markdown 형식으로 변경해주세요.

감사합니다! 이런 작은 조치들이 큰 도움이 되고, 정말 감사합니다!

YouTube: https://www.youtube.com/@zlliu246

LinkedIn: https://www.linkedin.com/in/zlliu/