오늘의 취미 코딩 연습에서 우리는 압축되지 않은 점성 유체에 대한 네비에-스톡스 방정식을 해결합니다. 이를 위해 스펙트럼 방법을 구현할 것입니다. 네비에-스톡스 방정식은 물과 같은 유체의 움직임을 대략적으로 설명합니다. 이 방정식은 난류 현상을 포착할 수 있습니다. 이 시스템은 수학에서 3D 해의 존재와 부드러움을 일반적으로 증명하는 것이 밀레니엄 상 문제 중 하나입니다.
GitHub에서 함께하는 Python 코드를 찾을 수 있습니다.
입도에 들어가기 전에 이 데모를 실행하는 것이 어떻게 되는지 보여주는 gif가 아래에 있습니다:

네비에-스톡스 방정식
비점성을 가진 점성도 ν로 주어진 불압축성 유체의 속도장 v(x)의 진화를 고려합니다. 이는 네비에-스톡스 방정식에 의해 지배됩니다:
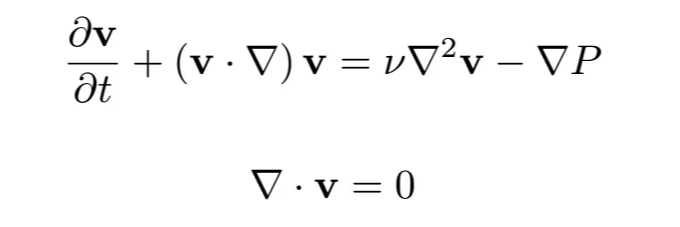
여기서 P는 유체압력을 나타냅니다. 불압축성 유체의 경우 압력장은 특별합니다: 시간에 따라 진화되는 별도의 변수가 아니며(압축성 유체의 경우와 달리), 압력은 속도장의 발산을 유지하는 해결책입니다(두 번째 방정식). 속도장은 압축을 일으킬 수 있는 비선형 항인 이송을 경험하며, 유체는 점도 계수 ν로 인한 확산도 경험합니다. 점도 계수가 클수록 유체는 꿀처럼 '끈적거리는' 특성을 갖습니다.
스펙트럼 방법
스펙트럼 방법은 편미분 방정식의 수치해를 전역 기저 함수의 합으로 표현하고, 이때 계수는 풀어야 하는 알려지지 않은 값으로 나타냅니다. 여기서 우리는 주기적 영역에 연속적인 해를 표현하는 데 이상적인 푸리에 기저를 고려할 것입니다. 이러한 방법은 그런 다음 빠른 푸리에 변환(FFT) 알고리즘을 사용하여 물리적 영역 x에서 해를 푸리에 공간으로 변환하며, 여기서 해는 각각 파동수 k에 의해 설명되는 파동의 합이 됩니다. 이러한 방법을 이전 자습서에서 시간 의존 슈뢰딩거 방정식을 해결하는 데 사용했습니다. 우리는 속도장의 푸리에 계수를 묘사하기 위해 '모자' 표기법을 사용합니다:
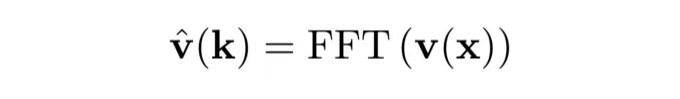
스펙트럼 방법을 특별하게 만드는 것은 무엇일까요? 한 가지 특별한 속성은 그래디언트 평가 및 관련 연산이 푸리에 공간에서 k에 의한 곱셈으로 전환된다는 것입니다. 예를 들어, 네비에-스토크스 방정식에 푸리에 변환을 적용할 때, 속도가 변환되는데:
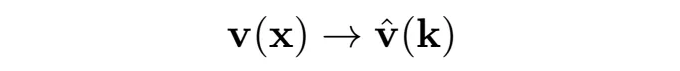
the gradient ∇ transforms as:
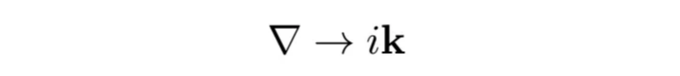
and the Laplacian transforms as:
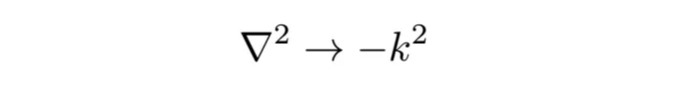
Thus, we can write functions to calculate operators like gradients, divergences, and curls of fields as follows:
Calculating the gradient ∇v using FFTs:
Calculating the divergence ∇.v using FFTs:
FFT를 사용하여 회전 ∇ x v를 계산하는 방법:
위의 함수들은 주기적인 함수의 미분을 계산하는 데 유용합니다. 이는 우리가 정의한 푸리에 공간 변수를 사용하는데, 그 중에는 모든 파동 수 k의 2D 배열이 포함됩니다:
이제 우리의 주된 스펙트럴 메소드를 개요로 설명해 보겠습니다. 다음으로 구성됩니다:
- 디바이션 필터 적용을 포함한 전진 오일러 단계를 사용하여 물리적 공간에서의 운반 단계
- 압력을 얻기 위해 푸리에 공간에서 포아송 문제 해결
- 유체 속도의 발산을 유지하기 위해 압력 기욥기를 적용하는 수정 단계
- 푸리에 공간에서의 확산 해결 (암시적 역 오일러)
알고리즘의 주요 루프는 다음과 같이 보입니다:
알고리즘 단계별로 진행해보겠습니다. 먼저, 비선형 이송 항의 효과를 계산합니다.
푸리에 공간에서 기울기를 계산할 때 저희 도우미 함수를 사용할 수 있지만, 곱셈은 물리적 공간에서 계산해야 합니다. 비선형 항은 경우에 따라 수치 문제를 일으킬 수도 있는데, 두 필드의 곱은 푸리에 기저에서 표현할 수 있는 최대 파동수보다 높은 파동수를 가질 수 있습니다. 이슈를 피하기 위해, 고주파 모드를 제거하기 위해 비앨리어싱 필터를 적용할 수 있습니다. 잘 알려진 2/3-룰을 사용하여 이를 수행합니다. 이 규칙에 따르면, 푸리에 기저에서 표현된 필드의 곱셈에 대해 기저에서 최대 파동수의 2/3 이하의 파동수만 신뢰할 수 있습니다. (참고: 2개 이상의 필드를 곱셈한다면 필터를 더 엄격하게 만들어야 합니다.) 따라서 필터를 구현합니다:
우리가 의해 정의 된 오른쪽 항을 가지고 있으면, 순방향 Euler 방법을 사용하여 시간 단계 n에서 시간 단계 n+1로 흐름 속도 필드를 진화시킬 수 있습니다:
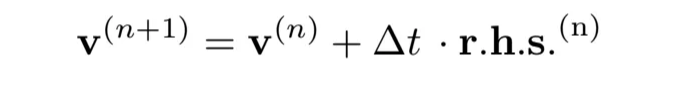
이 이동 단계는 속도 필드에 발산을 도입할 수 있으며, Navier-Stokes 방정식에서 압력의 역할은 이를 제거하는 것입니다. Helmholtz 분해 정리에 따르면, 어떤 벡터 필드도 벡터 A의 회전과 스칼라 P의 기울기의 합으로 분해될 수 있습니다. 다시 말해, 분해는 다음과 같이 보입니다:
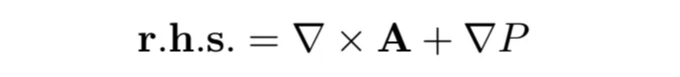
양쪽을 발산한 결과, A의 회전은 사라지고 다음과 같은 식이 남습니다:
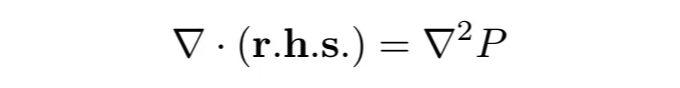
이는 포아송 방정식이며 P에 대해 풀 수 있습니다. 여기서 P는 실제로 유체 압력입니다! (표기법을 신중하게 선택했습니다.) P를 구하기 위해 푸리에 공간으로 변환하면 라플라스 연산자가 -k²가 됩니다. 빠른 포아송 솔버를 작성합니다:
P를 알면 그레디언트를 찾아 (푸리에 공간에서 ik로 곱셈) 속력 필드를 업데이트합니다:
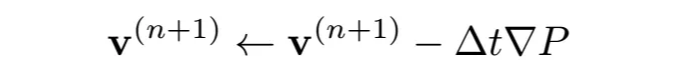
마지막 단계로, 확산 단계를 적용할 것입니다:
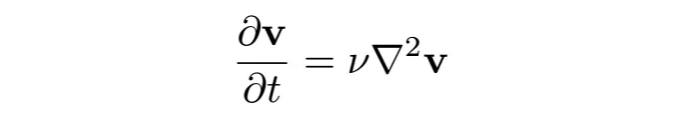
일반적으로 안정적인 타임 스텝 크기에 엄격한 제한이 있는 명시적 방법과 달리, 장시간 안정성을 갖는 암시적 방법을 사용하는 것이 좋습니다. 따라서 푸리에 공간에서 역 오일러 단계를 적용할 것입니다:
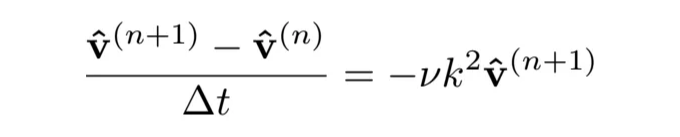
implemented as follows:
And there we have it! That’s it for the numerical method. Just a handful of lines at its core. Time to try it out!
Initial Conditions
우리는 2D 주기적 영역 [0,1]²에 간단한 테스트 문제를 구현합니다. 유체 필드는 낮은 파동수 회오리로 초기화됩니다. 진화는 전단력을 유발하고, 회오리의 형성으로 이어지며, 결국 점성으로 인해 소멸됩니다.
연습: 코드 효율성 향상
여기서 제시된 알고리즘은 내비에-스톡스 방정식의 서로 다른 부분을 해결하는 교육적 시연을 위해 설계되었습니다 (이동, 보정, 확산). 그러나 코드는 푸리에 변환을 중복하여 사용합니다 (예: 속도를 물리적 및 푸리에 공간 간에 변환하고 그래디언트를 계산할 때마다 다시 변환할 수 있습니다). FFT 호출 수를 최소화하여 코드 효율성을 향상시키는 것은 독자에게 맡겨둡니다.
코드를 실행하면 시뮬레이션을 실시간으로 시각화할 수 있고 유체의 회오리 (속도의 선의 회전)에 대한 그림을 얻을 수 있습니다:
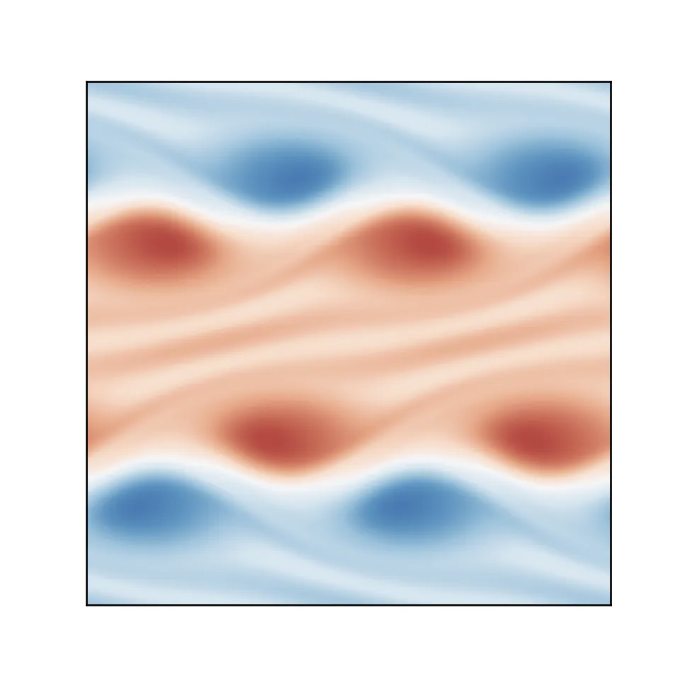
비압축성 네비에-스톡스 방정식은 다양한 수치 기법을 사용하여 해결할 수 있습니다. 유한 요소법, 유한 차이법, 스펙트럴 방법 및 격자 볼츠만 방법을 사용할 수 있습니다. 이러한 방정식을 시뮬레이션하는 것은 공학 분야에서 중요한 응용이 있습니다. 예를 들어, 비행기 설계는 비행기 전체에 이륜세기 유동을 시뮬레이션하는 기술의 혜택을 받을 수 있으며, 이러한 계산은 물리적 윈드 터널 실험이 필요 없게 할 수 있습니다.
네비에-스톡스 방정식은 이상화된 연속 유체를 설명하지만 현실을 완벽하게 표현하지는 못합니다. 예를 들어, 방정식은 경계 조건이 주어진 후 예외적인 경우에 뾰족한 모서리에서 무한한 속도를 예측할 수 있습니다(이른 ‘모서리 특이성’라고 함)! 방정식이 주기적 도메인에서 병렬사례에서 터질 수 있는지 여부는 수학에서 여전히 열려 있는 문제입니다. 그러나 네비에-스톡스 방정식은 높은 레이놀즈 수에 의해 특징 지어지는 유체 흐름에서 나타나는 복잡하고 혼돈스러운 행동인 난류의 복잡한 현상을 놀랍게도 포괄합니다.
네비에-스톡스 해법자의 Python 코드를 GitHub에서 다운로드하여 시뮬레이션을 실시간으로 시각화하고 초기 조건에 대해 실험해보세요. 즐기세요!
저자 소개
필립 모크는 로렌스 리버모어 국립 연구소의 계산 물리학자입니다. 그는 하버드 대학에서 학사 (’12) 및 박사 ('17) 학위를 받았으며, 박사 논문을 위해 천문학적 시스템의 고성능 컴퓨팅 알고리즘 및 시뮬레이션을 설계했습니다. 이 게시물이 마음에 드셨다면, 이야기에 👏박수를 보내 주시고, 다양한 과학 컴퓨팅 주제에 대한 파이썬 튜토리얼을 더 보시려면 저를 👉팔로우해주세요!