기계 학습의 기본 주제 중 일부가 여전히 연구자들에게 알려지지 않은 점은 놀랍습니다. 이러한 주제들은 기본적이고 흔히 사용되지만 여전히 신비로운 측면이 있다고 생각됩니다. 기계 학습에 대한 재미있는 점은 우리가 작동하는 것들을 만들고 나서 그것들이 왜 작동하는지 파악하는 것입니다!

여기서 저는 몇 가지 기계 학습 개념의 미지 영역을 조사하여, 이러한 아이디어가 기본적으로 보일지라도 사실은 여러 겹의 추상화로 이루어진 것임을 보여줍니다. 이는 우리가 지식의 깊이를 의심하는 연습을 할 수 있도록 도와줍니다.

이 글에서 우리는 신경망의 전통적인 이해를 도전하는 딥러닝의 중요한 현상 몇 가지를 탐구합니다.

• 먼저, 완전히 이해되지 않은 배치 정규화와 그 기본 메커니즘에 대해 알아봅니다.
• 우리는 과잉 매개변수 모델이 일반화를 더 잘 하는 상반된 기술적 기계 학습 이론에 반하는 현상을 검토합니다.
• 그래디언트 하강의 암묵적인 정규화 효과를 탐구하며, 신경망을 보다 단순하고 보다 포괄적인 솔루션으로 자연스럽게 편향시키는 것 같습니다.
• 마지막으로, 대규모 신경망에 작은 부분 네트워크를 포함하고 있는 복권 티켓 가설에 대해 언급해 봅니다. 이 가설에 따르면 훈련을 독립적으로 받을 때 비슷한 성능을 달성할 수 있는 더 작은 부분 네트워크를 포함하고 있습니다.

이 기사에는 4부분이 포함되어 있습니다. 그들은 서로 연결되어 있지 않기 때문에 원하는 부분으로 건너뛰어 읽어도 괜찮아요.

• 1. 배치 정규화
  • 우리가 이해하지 못하는 부분
  • 배치 정규화 고려 사항
• 2. 오버파라미터화와 일반화
  • 심층 학습의 이해는 일반화에 대한 재고가 필요합니다.
• 3. 신경망의 암묵적인 정규화
  • 실험 1
  • 실험 2
  • 경사 하강법은 자연 정규화기로 작용합니다.
• 4. 복권 티켓 가설
• 마지막으로.
  • 연락해요!
• 더 많은 읽을거리
• 참고 문헌

1. 배치 정규화

2015년 Sergey Ioffe와 Christian Szegedy에 의해 소개된 배치 정규화는 신경망을 더 빠르고 안정적으로 훈련시키기 위한 방법입니다. 이전에 입력 데이터를 평균이 0이고 분산이 1이 되도록 변환하면 수렴 속도가 더 빨라진다는 것이 알려져 있었습니다. 저자들은 이 아이디어를 더 발전시켜 입력층의 입력을 평균이 0이고 분산이 1인 것으로 변환하는 Batch Normalization을 소개했습니다.

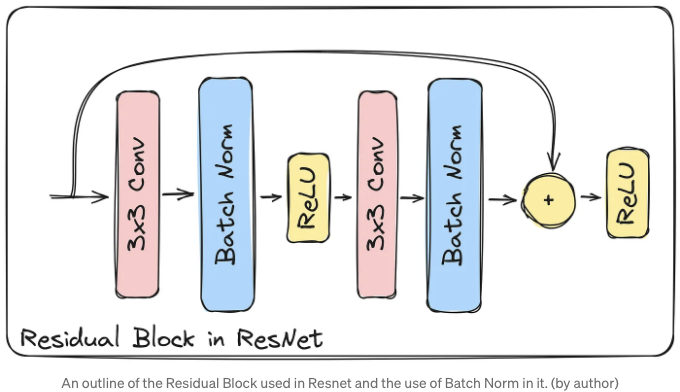
배치 정규화는 신경망에서 일반적으로 사용되는 기능으로 자리를 잡았습니다. 그 중 한 가지 예가 유명한 ResNet 구조에서 사용되는 것입니다. 따라서 우리는 그 효과를 확신할 만큼 효과적일 수 있다고 말할 수 있습니다.

배치 정규화의 효과에 대한 흥미로운 연구 [2]는 전체 ResNet-866 네트워크를 학습할 때 93%의 정확도가 나왔지만, 모든 파라미터를 동결하고 배치 정규화 계층의 파라미터만 학습할 때 83%의 정확도를 얻었다는 것을 보여줍니다. 이는 단지 10%의 차이입니다.

배치 정규화는 세 가지 측면에서 이점이 있습니다:

• 각 레이어의 입력을 정규화함으로써 학습 과정이 가속화됩니다.
• 초기 조건에 대한 민감도가 감소하여 조심스러운 가중치 초기화가 덜 필요합니다.
• 배치 정규화는 정규화기 역할도 합니다. 모델의 일반화를 향상시키고 경우에 따라 다른 정규화 기술이 필요하지 않을 수도 있습니다.

이해하지 못하는 부분

배치 정규화의 긍정적인 효과는 명백하지만, 누구도 그 효과적인 이유를 완전히 이해하고 있지는 않습니다. 배치 정규화 논문의 저자들은 배치 정규화를 내부 치프트 문제를 해결하기 위한 방법으로 소개했습니다.

내부 치프트에 대한 사전 경고는 처음에 상관없어 보이는 다양한 정의를 발견할 수 있다는 것입니다. 제가 정의하려는 방식을 여기에 나타내었습니다.

신경망의 계층은 완료(출력 계층)에서 시작(입력 계층)으로 역전파 중 업데이트됩니다. 내부 공변량 변화는 이전 계층의 매개변수가 업데이트됨에 따라 해당 계층의 입력 분포가 훈련 중 변경되는 현상을 가리킵니다.

내부 공변량 변화는 훈련 속도를 늦추고 네트워크가 수렴하기 어렵게 만들며, 각 계층은 이전 계층의 업데이트로 인해 입력 분포의 변화에 지속적으로 적응해야 합니다.

원래 배치 정규화 논문의 저자들은 배치 정규화의 효과를 내부 공변량 변화 문제를 완화시키는 데 있다고 믿었습니다. 그러나 나중에 나온 다른 논문은 배치 정규화의 성공은 내부 공변량 변화와 무관하며 최적화 Landscape를 부드럽게 만듦으로써 성공했다고 주장했습니다.

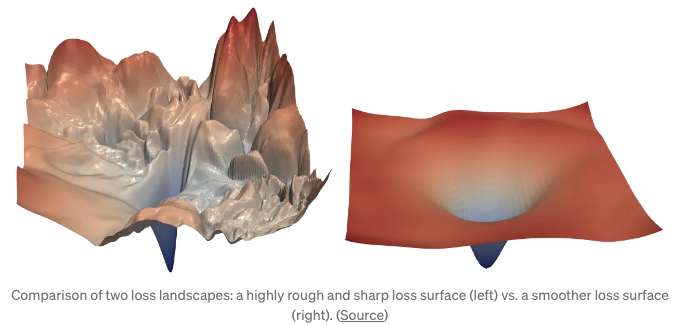
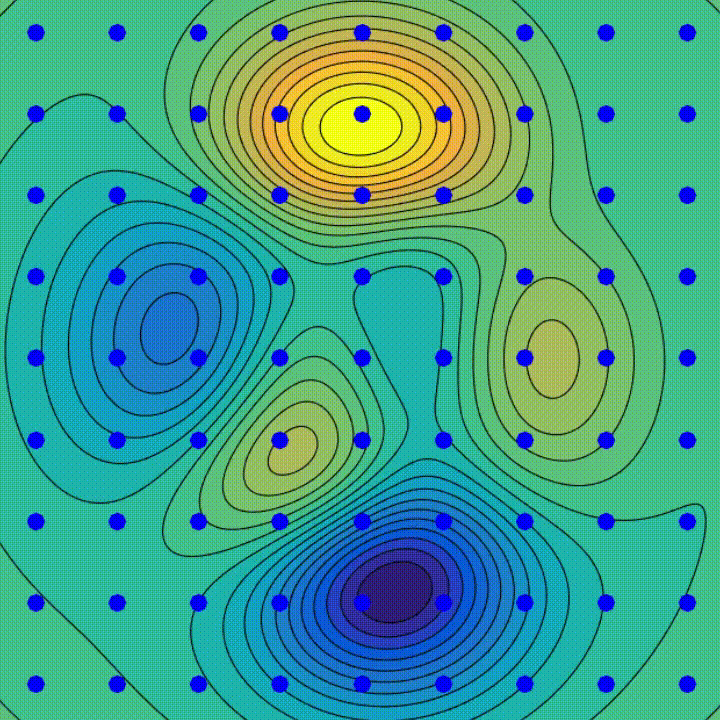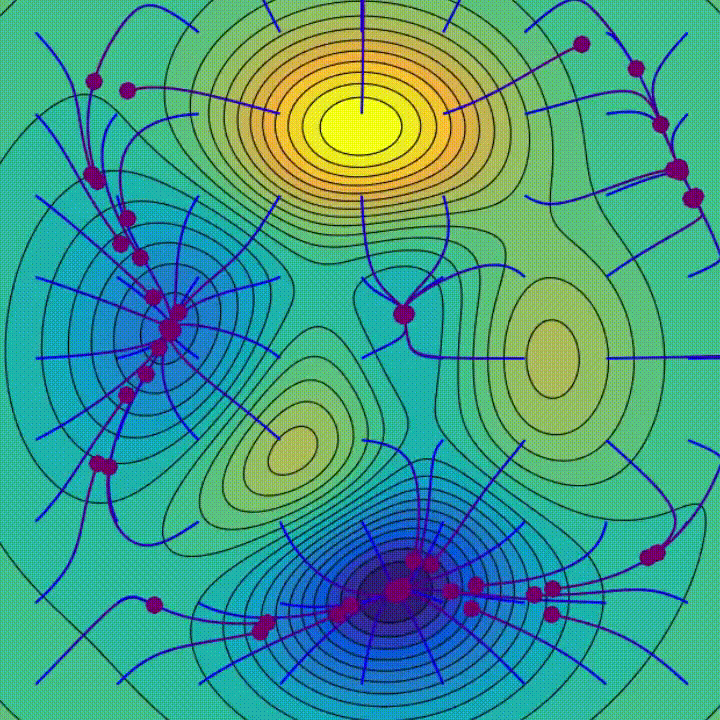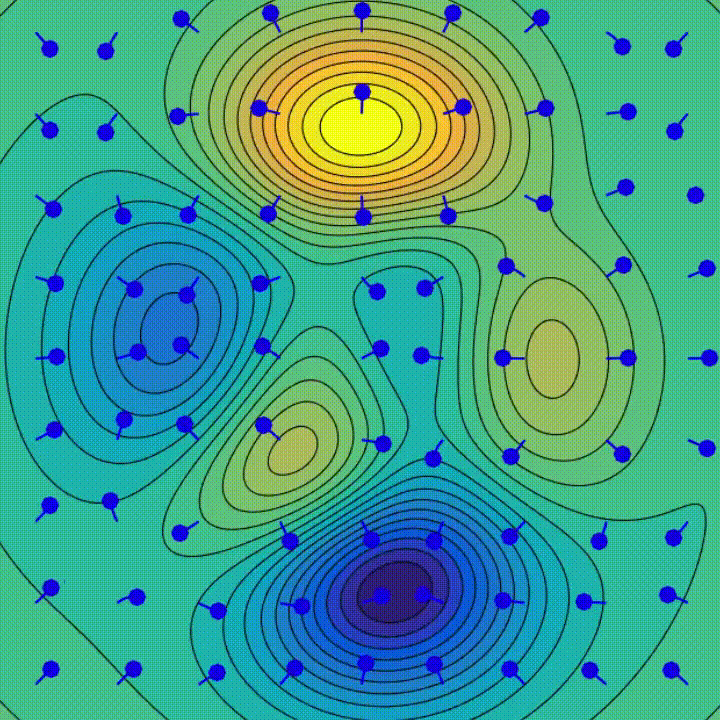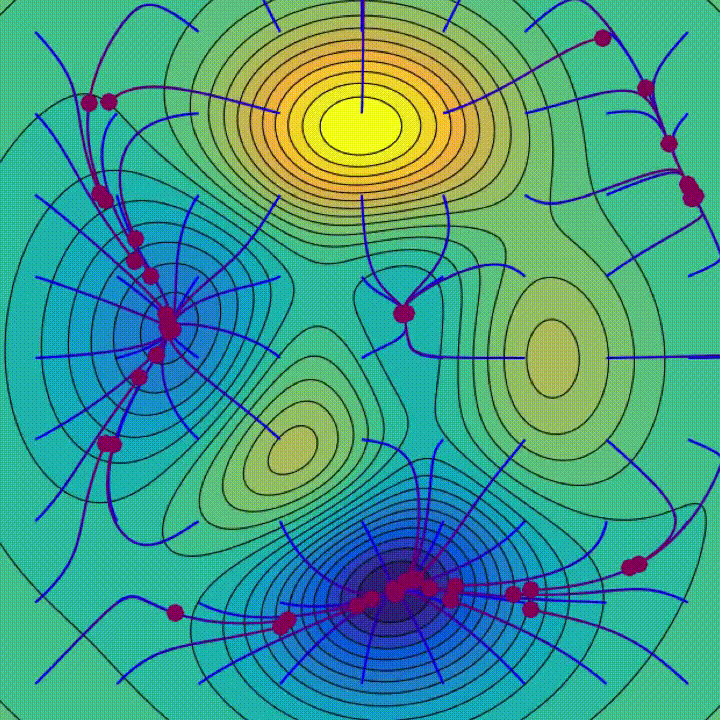
위의 그림은 Batch Normalization에 대해 실제로 다루지는 않지만 매끄러운 손실 지형이 어떻게 보이는지 잘 시각화한 것입니다. 그러나 Batch Norm이 효과적인 이유가 손실 지형을 매끄럽게 만드는 데 있다는 이론에는 고민과 의문이 있습니다.

Batch Norm 고려 사항

Batch Normalization이 어떻게 작동하는지에 대한 우리의 이해가 제한되어 있기 때문에 네트워크에 사용할 때 고려해야 할 사항은 다음과 같습니다:

• Batch Norm을 사용할 때 학습 및 추론 모드 간에 차이가 있습니다. 잘못된 모드 사용은 예상치 못한 동작을 일으킬 수 있으며 이를 식별하기 어려울 수 있습니다. [5]
• Batch Norm은 미니배치의 크기에 많이 의존합니다. 따라서 자세한 가중치 초기화가 덜 중요해지지만 올바른 미니배치 크기를 선택하는 것이 더 중요해집니다. [5]
• 활성화 함수 이전에 Batch Norm을 사용할지 또는 이후에 사용할지에 대해 여전히 논쟁이 진행 중입니다. [6]
• Batch Norm은 정규화 효과가 있지만, 드롭아웃이나 가중치 감쇠와 같은 다른 정규화와의 상호 작용은 명확히 알려지지 않았습니다.

Batch Norms에 대한 많은 질문이 있지만, 이러한 레이어가 신경망에 어떤 영향을 미치는지 밝히기 위한 연구는 아직 진행 중입니다.

2. 초매개변수화(Over-Parameterization)와 일반화(Generalization)

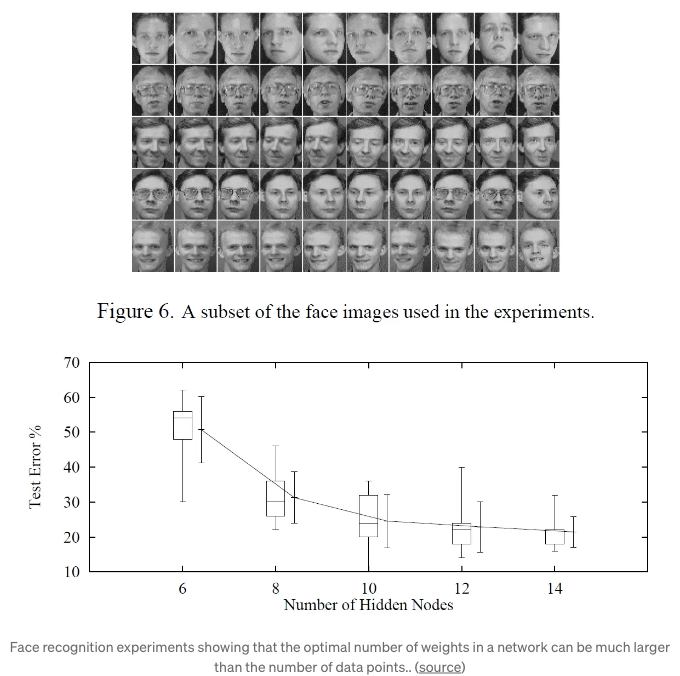
큰 네트워크들은 예전의 우리의 신경망 동작에 대한 믿음을 도전해왔습니다.

과거에는 과도한 매개 변수가 사용된 모델을 사용하면 오버피팅될 것으로 전통적으로 믿어졌습니다. 따라서 해결 방법은 네트워크의 크기를 제한하거나 훈련 데이터의 오버피팅을 방지하기 위해 정규화를 추가하는 것이었습니다.

놀랍게도, 신경망의 경우 더 큰 네트워크를 사용할수록 일반화 오차(|훈련 오류 - 테스트 오류|)가 개선될 수 있습니다. 다시 말해, 더 큰 네트워크가 더 잘 일반화됩니다. 이는 예를 들어 VC dimension과 같은 전통적인 복잡성 지표들이 약속했던 것과 모순됩니다.

이 이론은 또한 딥 신경망이 훈련 데이터를 기억하거나 패턴을 학습함으로써 성능을 달성하는지 여부에 대한 논쟁을 제기합니다. 데이터를 기억한다면, 어떻게 보이지 않는 데이터를 예측하기 위해 일반화할 수 있을까요? 그리고 데이터를 기억하지 않고 단지 근본적인 패턴을 학습한다면, 라벨에 일정량의 노이즈를 추가하더라도 올바른 라벨을 예측하는 방법은 무엇일까요?

딥 러닝을 이해하려면 Generalization에 대해 다시 생각해야 합니다

이 주제에 대한 흥미로운 논문은 'Understanding deep learning requires rethinking generalization' [10] 입니다. 저자들은 전통적인 방식이 왜 더 큰 네트워크가 잘 일반화되며, 동시에 이러한 네트워크는 심지어 무작위 데이터에도 맞출 수 있는지 설명하지 못하는 것으로 주장합니다.

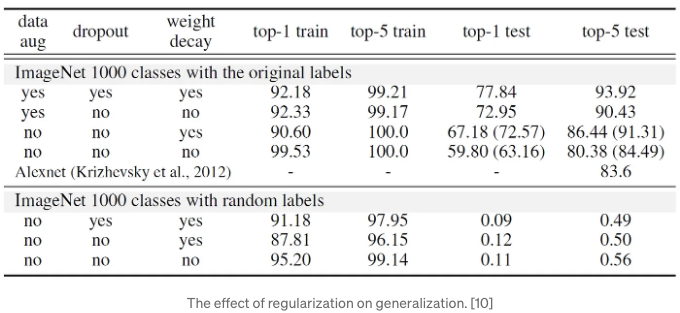
이 논문의 주목할 만한 부분 중 하나는 명시적 정규화인 weight decay, dropout 및 데이터 증가가 일반화 오차에 미치는 역할을 설명합니다:

Dropout 및 weight decay를 적용해도 InceptionV3는 여전히 무작위로 생성된 훈련 세트에 예상을 뛰어넘는 결과를 보였습니다. 이는 정규화를 가치 없게 하려는 것이 아니라, 모델 구조를 변경함으로써 더 큰 이득을 얻을 수 있다는 점을 강조하기 위한 것입니다.

그렇다면 일반화가 잘되는 신경망은 어떻게 구별될까요? 정체가 되지 않는 것 같네요. 몇 가지를 다시 생각해야 할 것 같습니다:

• 모델의 유효 용량에 대한 이해
• 모델의 복잡성과 크기를 측정하는 방법. 모델 파라미터나 FLOPs가 좋은 지표인가요? 분명히 아닙니다.
• 일반화의 정의와 측정 방법.

커다란 네트워크와 매개변수 개수가 일반화에 미치는 영향에 대해 다수의 논문과 블로그 포스트를 찾을 수 있습니다. 때로는 서로 모순되기도 합니다.

현재 우리가 이해한 바에 따르면, 더 큰 네트워크는 오버피팅되기 쉽지만, 깊이 덕분에 얕은 네트워크와 비교했을 때 더 복잡한 패턴을 학습할 수 있어 일반화가 잘 될 수 있습니다. 이는 대부분 도메인에 따라 다릅니다. 특정 데이터 유형은 작은 모델로부터 이점을 얻을 수 있으며 Occam의 면도날 원리를 따른 것일 수도 있습니다 (자세한 내용은 아래 게시물을 참고해주세요👇).

3. 신경망의 내재적 정규화

머신러닝의 핵심에는 Gradient Descent가 있습니다. Gradient Descent(GD)와 Stochastic Gradient Descent(SGD)는 머신러닝을 처음 시작하는 사람들에게 소화하기 쉬운 첫 번째 방법 중 하나입니다.

알고리즘은 직관적으로 보이기 때문에 그 깊이가 많지 않을 것으로 예상할 수 있습니다. 그러나 기계 학습에서는 수영장의 버튼을 결코 찾을 수 없습니다.

신경망은 경사 하강법에 의한 내재적 규제로 인해 더 간단하고 일반적인 해결책을 찾도록 밀어낼 수 있을까요? 이전 부분에서 보여진 것처럼 초매개변수화된 네트워크가 일반화하는 이유가 될 수 있을까요?

주의해야 할 두 가지 실험이 있습니다.

실험 1

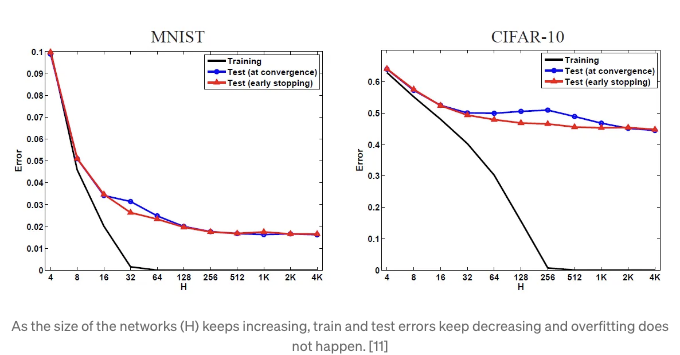
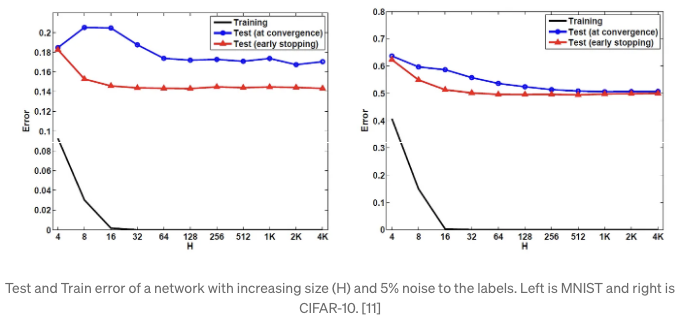
[11]에서의 저자들이 CIFAR-10과 MNIST 데이터셋을 사용하여 SGD와 명시적 규제 없이 모델을 훈련시킨 결과, 네트워크의 크기가 증가할수록 테스트 및 훈련 오차가 계속 감소한다는 결론을 이끌었습니다. 이는 더 큰 네트워크가 오버피팅으로 인해 더 높은 테스트 오차를 가진다는 믿음과는 반대됩니다. 더 많은 매개변수를 네트워크에 추가해도 일반화 오차가 증가하지 않습니다. 그런 다음 네트워크에 임의의 라벨 노이즈를 추가하여 네트워크가 오버피팅하도록 만들었습니다. 아래 그림에서 확인할 수 있듯이, 5%의 임의 라벨을 추가해도 테스트 오차가 더욱 감소하며 오버피팅의 현저한 징후가 없습니다.

실험 2

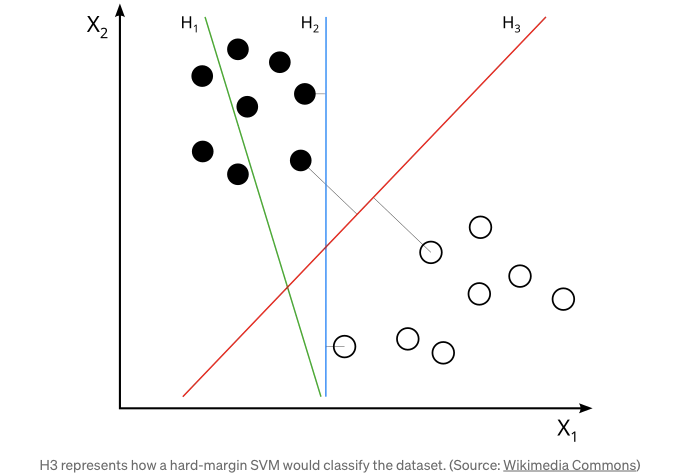
중요한 논문인 “In Search of the Real Inductive Bias [12]”에서는 선형 분리 가능한 데이터셋을 사용하여 예측기를 맞추는 실험을 진행했습니다. 저자들은 로지스틱 회귀를 사용하여 경사 하강법과 규제 없이 최대 여백 분리자(하드 마진 SVM으로도 알려짐) 방향으로 솔루션을 편향시키는 것을 보여주었습니다. 이는 경사 하강법의 흥미로운 그리고 놀라운 행동입니다. 손실 및 최적화가 마진 최대화를 장려하는 용어와 관련이 없다는 점에서 지지 벡터 머신에서 발견되는 것과 같은 용어와 직접적으로 관련이 없기 때문에 경사 하강법은 자연적으로 최대 여백 분류기 방향으로 솔루션을 편향시킵니다.

경사 하강법은 자연적인 정규화 방법

이 실험들은 최적화 과정이 더 간단하고 안정적인 솔루션을 선호하는 암묵적인 정규화 효과를 시사합니다. 이는 GD가 더 간단한 모델을 선호하며 종종 "플랫" 최소값이라고 하는 특별한 종류의 로컬 최소값으로 수렴하며, 이는 더 낮은 일반화 오류를 가진 경우가 많습니다. 이것은 왜 딥 러닝 모델이 종종 훈련 데이터 이상의 실제 작업에서 성능이 우수한지 설명해주는데 도움이 됩니다. 이것은 최적화 과정 자체가 암묵적인 정규화의 형태로 간주될 수 있음을 시사하며, 훈련 데이터에서 오류가 적은 모델을 생성할 뿐만 아니라 보이지 않는 데이터를 예측하는 데 강건한 모델을 만들어냅니다. 전체적인 이론적 설명은 아직 활발한 연구 분야입니다.

아마도 이 기사도 흥미로울 수 있을 거에요. 깊은 신경망이 현실의 통합된 표현으로 수렴하는 이유와 방법에 대해 말이죠:

4. 복권티켓 가설

모델 가지치기(pruning)는 훈련된 신경망의 매개변수를 90% 줄일 수 있습니다. 제대로 수행하면 정확도가 줄지 않은 채 이를 달성할 수 있어요. 다만, 모델을 가지치기할 수 있는 시점은 훈련 이후뿐이에요. 만약 불필요한 매개변수를 훈련 전에 제거할 수 있다면, 훨씬 적은 시간과 자원을 사용해도 된다는 뜻이죠.

복권티켓 가설[13]은 신경망에는 제대로 훈련되었을 때 원래 신경망과 비교 가능한 테스트 정확도에 도달할 수 있는 하위 신경망들이 포함되어 있다고 말해요. 이 하위 신경망들인 복권티켓은 초기 가중치가 그들의 훈련을 성공시키는 요인이라고 합니다.

저자들은 이러한 서브네트워크를 반복적인 가지치기 방법을 통해 찾습니다:

• 네트워크 훈련: 먼저, 원래 가지치기되지 않은 네트워크를 훈련합니다.
• 가지치기: 훈련 후, 가중치의 p%를 가지칩니다.
• 가중치 초기화: 남은 가중치는 초기 초기화 값으로 설정됩니다.
• 재훈련: 가지친 네트워크를 재훈련하여 이전 네트워크보다 동일하거나 더 높은 성능을 달성할 수 있는지 확인합니다.
• 반복: 원래 네트워크의 희박성이 원하는 수준에 도달하거나 가지친 네트워크가 더 이상 가지치기되지 않은 네트워크의 성능을 따라갈 수 없을 때까지 이 프로세스를 반복합니다.

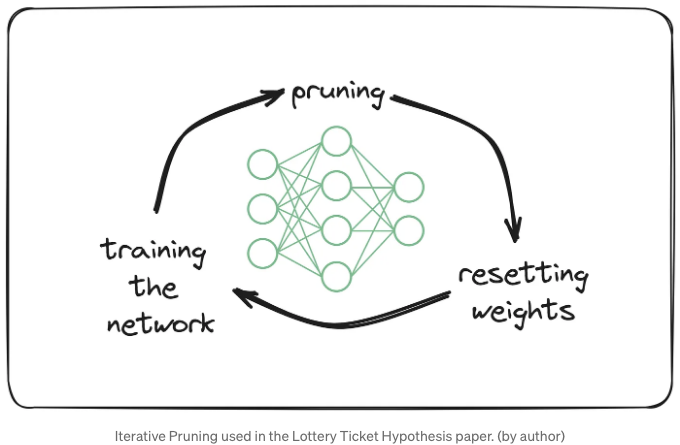
제안된 반복적 훈련 방법은 계산 비용이 많이 소요되며, 다수의 실험에서 네트워크를 15번 이상 훈련해야 합니다.

신경망에서 이러한 현상이 발생하는 이유는 아직 연구 중인 분야입니다. SGD가 네트워크를 훈련할 때 이기는 티켓에만 초점을 맞추고 네트워크 전체에는 주의를 기울이지 않을 수도 있을까요? 왜 일부 랜덤 초기화에는 이렇게 효과적인 하위 네트워크가 포함되어 있을까요? 이 이론을 깊이 있게 탐구하려면 [13]과 [14]를 놓치지 마세요.

마지막으로

기사를 읽어주셔서 감사합니다! 가능한 정확한 내용을 제공하기 위해 최선을 다해 노력했지만 필요한 수정 사항이 있다면 의견과 제안을 공유해 주세요.

함께 소통합시다!

무료로 구독하시면 새 기사 알림을 받을 수 있습니다! 또한 LinkedIn과 Twitter에서도 저를 만날 수 있어요.

더 읽어볼 거리

지금까지 읽으신 분들께는 아래 기사들도 흥미롭게 느껴질 수 있어요:

참고 문헌

1. Ioffe, S., & Szegedy, C. (2015). Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv.

2. Outside the Norm, DeepLearning.AI

3. Santurkar, Shibani; Tsipras, Dimitris; Ilyas, Andrew; Madry, Aleksander (29 May 2018). “How Does Batch Normalization Help Optimization?”. arXiv:1805.11604

4. Li, H., Xu, Z., Taylor, G., Studer, C., & Goldstein, T. (2018). Visualizing the Loss Landscape of Neural Nets. arXiv

| 5 | On The Perils of Batch Norm | | 6 | Link to Tweet | | 7 | Neyshabur, B., Li, Z., Bhojanapalli, S., LeCun, Y., & Srebro, N. (2018). Towards Understanding the Role of Over-Parametrization in Generalization of Neural Networks. arXiv. | | 8 | Why is deep learning hyped despite bad VC dimension? |

[9] DEEP NETS DON’T LEARN VIA MEMORIZATION

[10] Zhang, C., Bengio, S., Hardt, M., Recht, B., & Vinyals, O. (2017). Understanding Deep Learning Requires Rethinking Generalization. arXiv:1611.03530

[11] Neyshabur, B., Tomioka, R., & Srebro, N. (2015). In Search of the Real Inductive Bias: On the Role of Implicit Regularization in Deep Learning. arXiv:1412.6614

[12] Soudry, D., Hoffer, E., Nacson, M. S., Gunasekar, S., & Srebro, N. (2017). The Implicit Bias of Gradient Descent on Separable Data. arXiv:1710.10345

[13] Frankle, J., & Carbin, M. (2019). The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. arXiv:1803.03635

[14] https://www.lesswrong.com/posts/Z7R6jFjce3J2Ryj44/exploring-the-lottery-ticket-hypothesis