이미지 생성 분야에서 활기찬 시기에 Diffusion 모델을 중심으로 한 수학과 안정적 확산 모델 뒤에 숨겨진 직관에 초점을 맞추어 이 게시물에서 설명할 것입니다.
이 게시물은 노이즈 제거 확산 확률 모델 논문에서 보여진 것처럼 손실 함수가 이미지의 실제 노이즈와 예측된 노이즈 사이의 간단한 제곱 차이 용어로 귀결되는지 해석하는 것을 목표로 합니다.
변분 베이지안 방법의 증거 하한(Evidence Lower Bound, ELBO)이 개념과 단계를 상기하고 싶다면, 잠재 변수 모델과 확률적 주성분 분석에 대한 이전 상세 게시물을 확인해 주세요.
지체 없이 시작해 봅시다!
표기 및 정의:
몇 가지 표기부터 시작해보겠습니다.
x_0: 이는 시간 단계 0에서의 이미지를 나타냅니다, 즉 프로세스 시작 시의 원본 이미지를 의미합니다. 때로는 노이즈 제거 과정의 최종 단계에서 회복된 이미지를 가리킬 때도 있습니다.
x_T: 이는 최종 시간 단계에서의 이미지를 나타냅니다. 이 시점에서 이미지는 단순히 등방성 가우시안 노이즈입니다.
Forward Process: 이것은 여러 단계로 이루어진 과정이며, 각 단계에서 입력 이미지는 저수준의 가우시안 노이즈로 오염됩니다. 각 시간 단계 x_1, x_2, …., x_T 에서 얻은 잡음이 섞인 버전은 Markovian 과정을 통해 얻어집니다.
q(x_t | x_'t−1') ≡ 순방향 프로세스; 시간 단계 t-1에서 이미지가 주어지면 현재 이미지를 반환합니다.
마르코프 체인 (Markov Chain, MC): 다른 상태 간의 전이를 설명하는 확률 과정 ('메모리 없음')으로, 특정 상태로의 전이 확률은 오직 현재 상태 및 경과된 시간에만 의존하는 것을 참조합니다. 다음은 확률적 정의입니다:
임의의 양의 정수 n과 무작위 변수 X_1, X_2, X_3,…의 가능한 상태 x_0, x_1, x_2,…의 경우, 마르코프 특성은 n단계에서 현재 상태 x_n의 확률은 오직 그 전 단계 n-1에서의 상태에만 의존한다는 것을 말합니다.
Forward Process & MC:
데이터 분포 x0∼q(x0)가 주어졌을 때, 순방향 마르코프 과정은 전이 커널 q(x_t | x_'t−1')을 사용하여 랜덤 변수 x1,x2,…,xT의 시퀀스를 생성합니다. 확률의 연쇄 법칙과 마르코프 성질을 이용하여 다음과 같이 쓸 수 있습니다:
여기서 β는 0과 1 사이의 어떤 숫자이며, 즉 β∈(0,1)입니다. DDPM 논문(ref. 1)에서는 노이즈 스케줄이 선형이었습니다. 이는 고해상도 이미지에 대해서는 괜찮다는 것이 밝혀졌지만, ref. 3에서는 저해상도(예: 32×32)에 대해서도 작동하는 개선된 학습 스케줄을 제안했습니다. 일반적으로, β1 β2 β3 … βT이며, 각 시간 단계를 거칠 때마다 새로운 가우시안은 평균이 0에 근접합니다. 따라서 q(x_T | x_0) ≈ 𝒩(0,I)입니다. 요약하면, 순방향 과정은 모든 구조가 소멸될 때까지 데이터에 노이즈를 천천히 주입합니다.
순방향 과정의 단일 단계 정의를 고려하면, 100번의 프로세스 반복으로 100번째 시각 단계의 이미지에 도달할 수 있습니다. 그러나 노이즈를 반복 적용하는 대신, 특정 시간 단계에서만 하나의 단계를 사용하여 데이터 포인트를 샘플링할 수 있는 방법이 있다면 어떨까요? 즉, q(x_t | x_'t−1')이 알려져 있다면, q(x_t | x_0)에 대한 표현을 찾을 수 있을까요? 그럼 원본 이미지인 x_0에서 시작하여 주어진 시간 단계 t에서 노이지 이미지를 샘플링할 수 있을 것입니다.
Reparameterization Trick: The main idea comes from the fact that all normal distributions are basically scaled and shifted versions of 𝒩(0, I). When you have a normal random variable X, taken from a distribution with arbitrary μ & σ, you can express it as follows:

The proof of this trick is quite straightforward, and you can take a look at my notebook if you're interested later on. By using the reparametrization trick in Eq. 2, we can now consider an image at time step t:

x_t를 알고 있다면 (예를 들어 시간 t의 이미지), 시간 단계 t-1 및 t-2에서 이미지가 어떻게 되었는지 추정할 수 있을까요? 시작해 봅시다:
방정식 4에서 먼저 Eq. 3을 t를 t-1로 바꿔 다시 썼습니다 (두 번째 줄). 그런 다음 첫 번째 줄에서 x_'t-1'를 이 새로운 정의로 대체했습니다. 이 식을 조금 단순화할 수 있을까요? 네! 이를 위해 정규분포의 두 속성을 적용해 세 번째 줄에 도달할 필요가 있습니다. 이 두 속성은 다음과 같습니다:
방정식 4의 마지막 줄에 이 두 속성을 적용하면 다음과 같이 다시 쓸 수 있습니다:
Eq. 5에서 시간 단계를 점진적으로 감소시킬 수 있을까요? 여기서 x_t (시간 단계 t에서의 잡음 있는 이미지)를 x_0 (즉, 원본 이미지)을 기준으로 작성할 수 있을까요? 답은 예입니다. 아래는 그 방법입니다.
우리가 여기서 간단한 수학을 통해 달성한 것은 약간의 특별한 표현입니다: Eq. 3에서 시간 단계 t에서의 샘플링 프로세스가 t-1에서의 데이터를 필요로 했다면, Eq. 6에서는 1단계와 초기 입력 이미지만을 사용하여 어떤 단계에서든 데이터 포인트를 샘플링할 수 있습니다. 이제 순방향 과정이 크게 간소화되었고 어떤 시간 단계 t에서의 잡음 있는 이미지가 원본 이미지와 바로 연관되어 있음을 알 수 있습니다.
VAE에 관해서는, 우리는 순방향 과정을 데이터 인코딩 단계로 생각할 수도 있습니다; 그러나 Diffusion에서와는 달리, VAE의 경우 '고정된' 프로세스이며 신경망이 관련되지 않습니다; 데이터 공간에서 순방향 과정을 생각할 때, 데이터 포인트를 초기 데이터 분포에서 등방성 가우시안 잡음으로 밀어내는 과정으로 생각하고, 역 과정은 그 반대를 달성하려고 노력합니다; 역 과정에 대해 조금 더 자세히 알아보겠습니다;
역 과정:
전반적인 과정이 끝났을 때, 우리는 등방성 가우시안인 잠재 x_T를 가지게 됩니다. 우리가 정확한 역방향 분포 q(x_'t-1'|x_t)를 알고 있다면, 등방성 가우시안 노이즈 x_T ∼ 𝒩(0, I)에서 샘플링을 시작하여 과정을 역전시킬 수 있습니다(노이즈 제거) ;
하지만 q(x_'t-1'|x_t)를 추정하기 어렵기 때문에 베이즈 정리로 이를 확인할 수 있습니다;
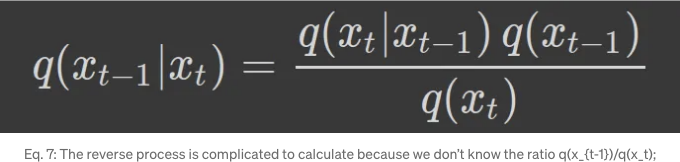
우리가 이미 전방 과정인 q(x_t|x_'t−1')을 알고 있다면, 역단계를 계산하려면 비율 q(x_'t−1')/q(x_t)을 알아야 합니다. 이것이 어려운 일이기 때문에 q(x_'t−1' | x_t)을 신경망으로 근사합니다. 하나의 분포를 다른 분포로 근사하는 것에 대해 생각할 때 우리의 마음은 이미 Kullback-Leibler 발산(KL divergence)과 가능한 가변 하한(variational lower bound)에 향할 것입니다.
역 과정은 LEARNED Gaussian 전환을 가진 MC로 정의되며, 역 과정에 대한 단일 단계는 다음과 같이 작성될 수 있습니다:
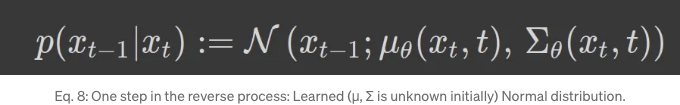
여기서 μ 및 Σ, 즉 평균과 분산 (다변량 정규 분포의 공분산 행렬)은 매개변수화되고 학습됩니다 (여기서 신경망이 등장합니다). DDPM 논문의 저자들은 공분산 행렬이 아래와 같은 특정 분산 일정으로 고정되었다고 가정했습니다:
위의 방정식에서 양 분산 일정은 유사한 결과를 제공했습니다. 따라서 남은 작업은 매개변수화된 평균 (μ)을 학습하는 것이며, 이 작업은 확산 모델에서 수행됩니다. 완전한 역 과정은 또한 아래와 같이 T까지의 단일 단계 역 과정의 곱과 시작점인 이소토픽 가우시안 노이즈 𝒩(0, I) ≡ p(x_T)의 결합 분포로 정의될 수 있습니다:
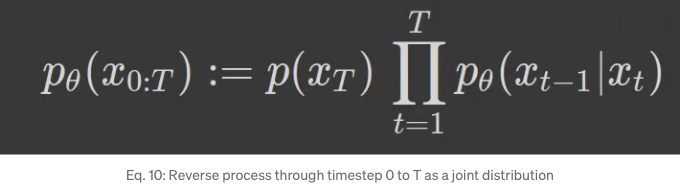
x1,…xT는 데이터와 차원적으로 동일한 잠재변수입니다. 즉, 노이즈를 적용하기 전과 후에도 이미지 크기는 동일합니다. 여기서 우리는 확산 모델을 VAE와 비교할 수 있습니다. 여기서 순방향 과정은 인코딩과 유사하다고 비교할 수 있으며 역방향 과정은 디코딩과 비교할 수 있습니다. 그러나 확산에서는 순방향 과정이 고정되어 있기 때문에 하나의 네트워크만 훈련해야 합니다. 반면에 VAE에서는 인코더와 디코더를 함께 훈련해야 합니다. 또한, 여기서 손실 함수의 유도와 VAE와 유사한 부분이 매우 잘 맞아 맞는 것을 볼 수 있습니다. 이것은 VAE와 비슷한 Latent Variable Models (LVMs)에도 맞는다는 것이며, 이는 이전에 가우시안 혼합 모델의 맥락에서 이야기했던 증거 하한(Evidence Lower Bound, ELBO)과 일반적으로 함께 다닌다는 것을 보여줍니다.
최소화하고 싶은 것은 -log p_θ (x_0)일 것입니다; 여기서 p_θ는 매개변수화된 분포이고 x_0은 시간 단계 0의 이미지입니다.
−log p_θ (x_0)을 최소화하는 것은 쉽게 계산할 수 없는 양이며, 그 이유는 x_0이 모든 다른 시간 단계 x1, x2, ... xT에 따라 달라질 수 있기 때문입니다. 매우 구체적으로 말하자면 우리는 계산하기 어려운 적분을 수행해야 합니다.
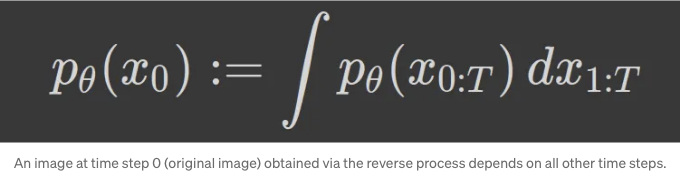
p_θ (x_0)를 얻기 위해서는 모든 다른 시간 단계에 대해 여러 가능한 방법으로 노이즈 제거된 이미지에 도달하는 것을 주변화해야 합니다. 이것은 단순히 불가능합니다(무한한 방법이 있을 수 있습니다); 여기서 로그-우도의 하한을 얻기 위해 증거 하한(Evidence Lower Bound)을 사용할 수 있습니다. LVMs와 확률론적 PCA의 맥락에서 ELBO를 토론했으므로 여기에서 정의를 사용해 봅시다: 우리가 우도(log p(x))를 계산하는 과정에서 계산이 어려운 잠재 변수 z에 대한 사후분포 p(z|x)를 계산해야 할 경우, z를 다른 간단한 매개변수화된 분포 q(z|x)를 통해 근사화할 수 있습니다.
위의 식을 수학적인 조작을 통해 재작성하는 것도 가능합니다(참조로 제 노트북을 확인해 보세요) 위와 같이 KL Divergence를 사용하여:
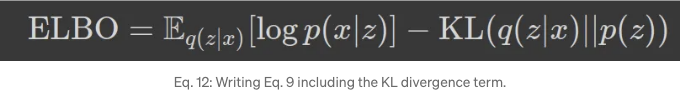
이 표현식 (방정식 12)을 사용하여 손실 함수를 유도할 것입니다; 확산 모델에서 x0(타임스텝 0의 이미지)은 참 데이터를 나타내고 x1, …, xT는 잠재 변수, 즉 x_'1:T'입니다; 이를 방정식 10에 사용해 봅시다:
위 식에서 q(x_'1:T'|x_0)를 q로 간략하게 표기했습니다. 또한 두 번째 단계에서 KL 발산의 정의를 사용했습니다. ELBO에 대한 위 식이 두 분포의 비율의 로그를 포함하고 있는 것을 알고 있기 때문에 (방정식 2 및 방정식 9에서), 우리는 여기서 그것들을 그대로 사용할 것입니다:
여기서 (방정식 14)는 정방향 및 역방향 프로세스의 정의를 사용하고 3개의 서로 다른 용어를 분리했습니다. t=1에 대한 용어를 분리하고 t≥ 2의 모든 용어를 그룹화한 이유는 곧 명확해질 것입니다.
만약 우리가 총합 항을 살펴보면, 분자는 역과정을 나타내지만 분모는 여전히 정방향 프로세스입니다; 역과정으로 바꾸려면 약간의 변형이 필요한데, 여기서 베이즈 이론(Eq. 7)을 활용할 수 있습니다; Eq. 7의 오른쪽 항들은 원본 이미지가 무엇이었는지 실제로 알기가 매우 어려울 정도로 높은 분산을 가지고 있습니다. 왜냐하면 역과정이 등방성 가우시안 잡음에서 시작되기 때문입니다. 따라서 저자들은 이 분포들을 원본 이미지 (x_0)로도 조건부로 만들었습니다:

이제 이를 총합 항의 분모 대체물로 Eq. 14에 사용할 수 있습니다:
특히 기대값 내에서 정방향 프로세스의 비율로 나타나는 두 번째 총합 항에 주목하며, 이를 간소화할 수 있습니다; 이를 보려면 T=5까지만 총합을 고려해 보겠습니다:
이게 대단해요. 이 용어가 결국 log q(x_1 | x_0)/q(x_T | x_0)로 수렴한다는 걸 말해줍니다. 이를 통해 우리는 다시 한 번 방정식 16로 돌아갈 수 있어요.
이 단계에서 우리는 로그 곱셈과 합침 법칙을 사용하여 식을 더 간단하게 만들 수 있어요.
첫 번째 항을 살펴봅시다. p(x_T)와 q(x_T|x_0)를 비교하는데, 정의에 따라 순방향 프로세스는 미리 정의되어 있으며 최종 x_T가 순수 가우시안인 것을 알 수 있어요. 따라서 이 항은 본질적으로 매개변수가 없고, 완전히 무시할 수 있어요. 또한, 이 항은 q(x_T|x_0) ≈ 𝒩(0, I)=p(x_T)이므로 거의 0에 가까울 것입니다.
두 번째 항은 실제 역과정을 비교하는 부분이에요, 즉 q(x_'t−1'|x_t, x_0) (x_0에 대한 조건부)과 매개변수화된 p_θ(x_'t−1'|x_t)을 비교하는 것에는 유의할 점이 있어요. 첫째로, 우리는 모든 단계에서 이 작업을 수행해야 해요. 둘째로, Lilian의 블로그에서는 q(x_'t−1'|x_t, x_0)이 원본 데이터 지점을 조건부로하고 가우시안일 때 근본적인 결과를 보여주었는데요. 따라서 우리는 q(x_'t−1'|x_t, x_0)의 정의를 정규 분포를 이용하여 가지고 있으며, 아래와 같습니다:
그래서 두 번째 항목에서 분모는 가우시안이고 분자는 정의에 따라 (방정식 8) 가우시안이기 때문에 두 개의 가우시안 분포를 비교하고 있습니다.
β~ 항목을 살펴보겠습니다. 이는 학습 속도 일정에만 의존하고 입력 이미지에는 의존하지 않습니다. 그래서 이제 우리의 초점은 μ~에 놓입니다.
네트워크가 방정식 8의 μθ(x_t, t)를 μ와 가능한 가깝게 예측하도록 원합니다. x0에 의존성을 제거하기 위해 μ 항목을 좀 더 단순화하여 시작 이미지 x0에 대한 의존성을 제거하겠습니다. 이를 위해 방정식 6의 xt로 x0을 교체하여 시작합니다:

x0을 Eq. 20에 다시 사용하여 μ~을 계산하면 다음과 같습니다:

여기에 도달하기 위한 단계들은 조심스러운 고려가 필요합니다. 아래에 자세한 단계들이 나와 있습니다. (스스로 시도한 후 노트북을 확인하는 것을 추천합니다)
Eq. 22의 수식은 정말 멋지죠! 우리 네트워크는 현재 단계의 이미지에서 잡음(랜덤 스케일)을 빼는 것을 반영하여 Eq. 8부터 μθ(x_t, t)을 예측하려고 노력하고 있습니다. Eq. 22!! 와우!!!
이미 저자들이 매개변수화된 정규 분포의 공분산을 β~로 고정했다는 것을 논의했습니다. 정규 분포를 지수 형태로 작성하고 이 두 분포의 비율의 로그를 취하여 (이는 KL 발산의 정의이기도 합니다) 방정식 19과 같이 한다면, 우리는 평균 제곱 오차와 같은 용어를 얻게 되며, 특정 시간 단계 t에 대해 다음과 같이 쓸 수 있습니다:
이 용어는 문헌에서 denoising matching 용어라고 불립니다. 우리는 추적 가능한, 정답인 denoising 전이 단계에 대한 근사값으로 원하는 denoising 전이 단계를 학습합니다. 여기서 C는 매개변수 θ와 독립적인 상수 용어입니다. 한번 더 강조하자면: 저희 네트워크는 전진 과정의 사후 평균을 예측하려고 노력하고 있습니다. 논문에서 직접 인용하면 "그래서, 우리는 가장 직접적인 µθ의 매개변수화가 μ˜, 즉 전진 과정 사후 평균을 예측하는 모델임을 알 수 있습니다." 이것은 매우 중요합니다.
더해, 방정식 23을 더욱 의미 있는 결론으로 단순화할 수 있습니다; 전진 과정의 사후 평균이 방정식 22에 주어진 형태임을 고려하고, 교육 중에 x_t가 사용 가능한 경우, 우리는 노이즈 용어 ϵ에만 집중합니다. 먼저, μθ를 μ~의 형태로 매개변수화합니다.
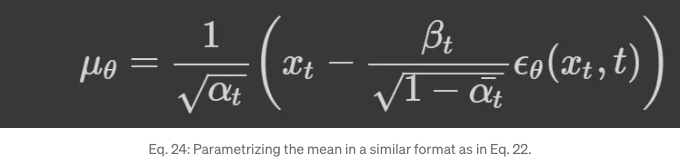
만약 우리가 방정식 24와 방정식 22에서의 μθ와 μ~의 표현을 방정식 23에 사용하면, 다음을 얻을 수 있어요:
여기서 모든 것은 시간 t에서 예측된 잡음과 실제 잡음 사이의 차이를 제곱으로 구하는 것으로 요약됩니다.
논문에서 인용하자면¹:
저자들은 또한 훈련이 더 좋아진다고 발견했어요 만약 우리가 가중치 항을 완전히 무시한다면.

파라미터화된 μθ의 정의가 방정식 24에 있기 때문에, 이를 방정식 8에 사용할 수 있습니다. 이제 재매개화 트릭의 정의(위의 내용 참조)를 사용하여 방정식 27에서 정규 분포에서 x_'t-1'을 샘플링하는 방법을 작성할 수 있습니다.
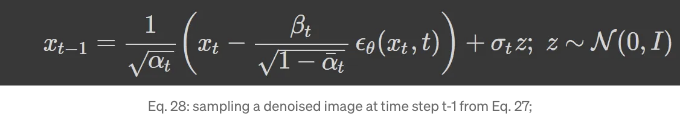
ELBO에 대한 또 다른 용어가 남아 있습니다. Eq. 19에서 마지막 용어는 log pθ(x_0 | x_1)입니다. 이 용어에 대해서 어떻게 생각하시나요? 저자들은 결국 이 용어를 무시했지만, 우리는 논문에 제시된 방정식 (즉, 아래 Eq. 29)에 대한 직관을 형성해보려 합니다. 저자들은 이미지를 [-1, 1]로 스케일링하고 (픽셀 값은 [0, 1] 사이) 이를 통일성 있게 만들었습니다. 이는 역 과정인 p(x_T)의 매우 초기 단계에서부터 시작되며, 여기서 샘플링은 평균이 0이고 분산이 1인 균일 가우시안에서 시작됩니다. 그런 다음 저자들은 다음과 같이 정의합니다:
여기서 D는 데이터 차원입니다 (이미지가 주어졌을 때, 해당 이미지의 전체 픽셀 수). δ+, δ−는 원래 픽셀 값(xᶦ_0)의 범위 주변에서 통합함을 나타냅니다. 만약 μᶦ_θ가 픽셀의 평균 값에 가깝다면, 통합 결과는 크게 나타날 것입니다 (다른 모든 픽셀에 대해 예측이 좋다고 가정).
아래 코드 블록을 살펴봅시다: 처음에 β가 매우 낮은 값 (0.0001)인 것을 알고 있고, 이미지(x0) 내에서 픽셀 값이 87/255일 때, 첫 번째 단계에서 노이즈를 추가하면 픽셀 값이 89/255가 됩니다. 우리의 노이즈 제거 네트워크는 이 과정을 되돌리려고 시도하고, 예측된 픽셀 값이 좋다면 μ_'x1, 1' = 88/255로 예측되거나 나쁘다면 μ_'x1, 1' = 93/255로 예측됩니다. 그래서 먼저, 예측된 값에서 평균이 μ_'x1, 1'인 정규 분포에 대해 생각해봅시다. 그리고 우리의 통합 한계는 ±1이 됩니다. 즉, 87/255 주변의 참 픽셀 값인 [87/255 − 1/255, 87/255 + 1/255]입니다 (위의 방정식 내 δ+ , δ−의 정의를 살펴봅시다).
예측이 좋을 때 우리는 PMF가 높을 것이며, 진실에서 멀리 떨어진 예측일 때는 PMF가 낮을 것입니다. 그래서 이 용어는 네트워크 예측이 모든 픽셀에 대해 좋을 때에만 기여합니다 (곱셈 용어이기 때문에). 코드를 작성하고 결과를 그래프로 표현해봅시다:
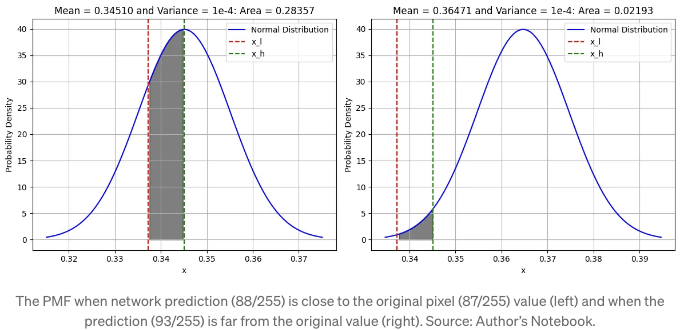
Eq. 29이 전달하려고 하는 메시지를 이해하는 데 도움이 됩니다. 저자들은 최종 손실에서 이 용어를 제거하고 결국 모든 것이 아래의 방정식으로 정리됩니다.
위의 방정식에서는 Eq. 6에서 x_t의 정의를 사용했습니다.
마지막으로, 저자들은 자신들의 확산 과정 설정에서, t의 값이 작을 때 손실 항을 Eq. 30에서 가중치를 낮춘다는 점을 강조했습니다. 즉, 노이즈가 적을 때입니다. 이것은 네트워크가 더 많은 어려운 더놄 작업에 집중하도록 배우게하기 때문에 유익합니다. 목적 함수(Eq. 30)의 재가중치화는 더 나은 샘플링으로 이어집니다.
한 순간 멈춰서, 다소 정교한 증거 하한(Evidence Lower Bound)에서 시간 단계 t에서의 원래 오리지널 및 예측된 노이즈를 처리하는 간단한 손실 용어로 이르기까지 계산에 포함된 복잡한 세부 사항들을 감상해 봅시다.
이것이 도움이 되었으면 좋겠습니다. 현대 딥러닝에서 수학이 왜 중요한지 진정으로 이해할 수 있을 겁니다.
참고 자료:
[1] 'Denoising Diffusion Probabilistic Models': J. Ho, A. Jain, P. Abbeel
[2] 확산 모델이란 무엇인가요? Lilian Weng.
[3] 개선된 노이즈 제거 확산 확률 모델: A. Nichol, P. Dhariwal arXiv: 2102.09672
[4] 확산 모델 이해: 통합적인 관점: C. Luo arXiv: 2208.11970.
[5] 제 노트북 및 노트: GitHub 링크.
참고: 모든 이미지는 저자가 제작했습니다!